Comprensión de la estadística
La Estadística es la parte de las Matemáticas que se encarga del estudio de una determinada característica en una población, recogiendo los datos, organizándolos en tablas, representándolos gráficamente y analizándolos para sacar conclusiones de dicha población.
Otras definiciones
Murray y Spiegel
La estadística estudia los métodos científicos para recoger, organizar, resumir y analizar datos así como para obtener conclusiones válidas y tomar decisiones razonables basadas en tal análisis.
Daniel Peña
La estadística actual es el resultado de la unión de dos disciplinas que evolucionaron independientemente hasta confluir en el siglo XIX: La primera es el cálculo de probabilidades que nace en el siglo XVII como teoría matemática de los juegos de azar. La segunda es la estadística (o ciencia del Estado, del latín status), que estudia la descripción de datos y tiene raíces más antiguas. La integración de ambas líneas del pensamiento da lugar a una ciencia que estudia cómo obtener conclusiones de la investigación empírica mediante el uso de modelos matemáticos.
Mendenhall
La estadística es un área de la ciencia que se ocupa del diseño de experimentos o procedimientos de muestreo, del análisis de datos y de realizar inferencias acerca de una población de mediciones a partir de la información contenida en una muestra.
Deducción
La estadística es una rama de la ciencia matemática que se ocupa de organizar, resumir y analizar datos y, partiendo de ese análisis, realiza inferencias (deducciones) de una población a partir de la información contenida en una muestra. La estadística, en una etapa más avanzada, trata de obtener conclusiones válidas para la toma de decisiones en una investigación mediante el uso de modelos matemáticos, en economía recibe el nombre de econometría.
ANTECEDENTES HISTÓRICOS
• En las pirámides de Egipto se encontraron pinturas que muestran juegos de azar, provenientes de la primera dinastía (3500 a.n.e.).
• Los dados más antiguos que se han encontrado se remontan a unos 3000 años a.n.e., y se utilizaron tanto en el juego como en ceremonias religiosas. Los oráculos, sacerdotes o pitonisas de Grecia y Roma, utilizaban la configuración resultante de tirar cuatro dados para predecir el futuro y revelar la voluntad favorable o desfavorable de los dioses.
• El cálculo de probabilidades se consolida como disciplina independiente en el periodo que transcurre desde la segunda mitad del siglo XVII hasta comienzos del siglo XVII. Durante el siglo XVIII, el cálculo de probabilidades se extiende a problemas físicos y actuariales (seguros marítimos). El principal impulsor de su desarrollo durante ese periodo es el conjunto de problemas de astronomía y física que surgen ligados a la contrastación empírica de la teoría de Newton (1642-1782).
• D. Bernoulli (1700-1782) proporciona la primera solución al problema de estimar una cantidad desconocida a partir de un conjunto de mediciones de su valor que, por el error experimental, presentan variabilidad.
• Otros importantes autores que contribuyen al desarrollo de la estadística son: Marqués de Laplace (1749-1827), Bravais (1846) y el geólogo y astrólogo Benjamín Pierce (1852).
• Por tanto, a mediados del siglo XIX existen ya las herramientas básicas que van a dar lugar a la estadística actual. Sin embargo, la aplicación de estos principios se restringió a la física y la astronomía con poca influencia sobre otras áreas del conocimiento.
• Paralelamente a este desarrollo de las herramientas estadísticas se daba el hecho de que desde la antigüedad los estados recogían la información sobre la población y la riqueza que existía en sus dominios. Los censos romanos, los inventarios de Carlomagno sobre sus posesiones, etc., pueden considerarse precedentes de la institucionalización de la recolección de datos demográficos y económicos por los estados modernos.
• Durante el siglo XVIII y la mayor parte del siglo XIX, la estadística evoluciona como ciencia separada del cálculo de probabilidades y la teoría de errores, es decir, en este caso se refiere a la estadística que se dedicaba a la recolección de información.
• La revolución realizada en la física por Newton, se produjo en la biología por la obra de Darwin. El primero en resaltar la necesidad de acudir a métodos estadísticos para contrastar la teoría de Darwin fue Francis Galton (1822-1911). Galton estudió exhaustivamente la distribución normal e introdujo el concepto de línea de regresión comparando las estaturas de padres e hijos.
• La solución de los problemas planteados por Galton y retomados por Weldon (1860-1906) requería de métodos estadísticos más avanzados que los existentes, razón por la cual, Weldon busca la colaboración de un matemático y filósofo: K. Pearson (1857-1936). La colaboración de estos autores y el apoyo de Galton constituyen el impulso generador de la corriente de contribuciones que dan fundamento a la estadística actual.
• El gran impulso se produce entre 1920 y el final de la Segunda Guerra Mundial, cuando se extiende la aplicación de los métodos estadísticos en áreas tan diversas como la ingeniería, la física, la antropología, la psicología y la medicina. La búsqueda de respuestas a las nuevas interrogantes planteadas por estas aplicaciones impulsan, a su vez, el desarrollo de nuevos métodos estadísticos.
• Durante este periodo las aplicaciones de la estadística a la economía conducen a una disciplina con contenido propio: la econometría.
• A partir de 1950 podemos considerar que comienza la época moderna de la estadística.
Clasificación
Estadística descriptiva. Realiza el estudio sobre la población completa, observando una característica de la misma y calculando unos parámetros que den información global de toda la población.
Estadística inferencial. Realiza el estudio descriptivo sobre un subconjunto de la población llamado muestra y, posteriormente, extiende los resultados obtenidos a toda la población.
Conceptos básicos
POBLACIÓN: Es el conjunto de elementos, individuos o entes sujetos a estudio y de los cuales queremos obtener un resultado.
Población finita: cuando el número de elementos que la forman es finito, por ejemplo el número de alumnos de un centro de enseñanza, o grupo clase.
Población infinita: cuando el número de elementos que la forman es infinito, o tan grande que pudiesen considerarse infinitos.
Al hacer un estudio de una determinada población, observamos una característica o propiedad de sus elementos o individuos. Cada una de estas características estudiadas se llama variable estadística
Por ejemplo: El número de hermanos, la estatura, peso, edad, profesión etc.
Variable cualitativa.
Es aquella característica que no podemos expresar con números y hay que expresarla con palabras. Por ejemplo, el lugar de residencia, comida favorita, profesión que te gusta,
Ordenables: Aquellas que sugieren una ordenación, por ejemplo la graduación militar, el nivel de estudios, etc.
No ordenables: Aquellas que sólo admiten una mera ordenación alfabética, pero no establece orden por su naturaleza, por ejemplo el color de pelo, sexo, estado civil, etc.
Variable cuantitativa.
Es cualquier característica que se puede expresar con números. Por ejemplo, el número de hermanos , la estatura, número de alumnos en tu instituto.
Discreta. Es aquella variable que puede tomar únicamente un número finito de valores. Por ejemplo, el número de hermanos.
Ejemplo: Tengo diez hermanos
Continua. Es aquella variable que puede tomar cualquier valor dentro de un intervalo real. Por ejemplo, la estatura.
Ejemplo: estatura entre 1.40m y 1.90m
Al numero de veces que se repite un cierto valor de nuestras variables se denomina frecuencia absoluta.
Se representa por 𝑓_𝑖.
La suma de las frecuencias absolutas es igual al número total de datos, que se representa por 𝑁.
Ejemplo:
calificaciones de un grupo de 50 alumnos
1-6-8-8-2-2-3-4-5-10-3-4-5-6-7-8-9-7-7-6-5-5-5-4-4-5-6-7-10-4-1-2-5-5-6-6-7-4-5-6-5-4-6-7-6-5-4-3-4-5
El valor de la frecuencia absoluta de la calificación 5 es 12 porque el CINCO se repite doce veces.
Formas de representación de información estadística
En los análisis estadísticos, es frecuente utilizar representaciones visuales complementarias de las tablas que resumen los datos de estudio. Con estas representaciones, adaptadas en cada caso a la finalidad informativa que se persigue, se transmiten los resultados de los análisis de forma rápida, directa y comprensible para un conjunto amplio de personas.
Tipos de gráficas
Cuando se muestran los datos estadísticos a través de representaciones gráficas, se ha de adaptar el contenido a la información visual que se pretende transmitir. Para ello, se barajan múltiples formas de representación:
Diagramas de barras: muestran los valores de las frecuencias absolutas sobre un sistema de ejes cartesianos, cuando la variable es discreta o cualitativa.
Histogramas: formas especiales de diagramas de barras para distribuciones cuantitativas continuas.
Polígonos de frecuencias: formados por líneas poligonales abiertas sobre un sistema de ejes cartesianos.
Gráficos de sectores: circulares o de tarta, dividen un círculo en porciones proporcionales según el valor de las frecuencias relativas.
Pictogramas: o representaciones visuales figurativas. En realidad son diagramas de barras en los que las barras se sustituyen con dibujos alusivos a la variable.
Cartogramas: expresiones gráficas a modo de mapa.
Pirámides de población: para clasificaciones de grupos de población por sexo y edad
Diagramas de barras e histogramas
Los diagramas de barras se usan para representar gráficamente series estadísticas de valores en un sistema de ejes cartesianos, de manera que en las abscisas se indica el valor de la variable estadística y en las ordenadas se señala su frecuencia absoluta.
Estos gráficos se usan en representación de caracteres cualitativos y cuantitativos discretos. En variables cuantitativas continuas, se emplea una variante de los mismos llamada histograma.
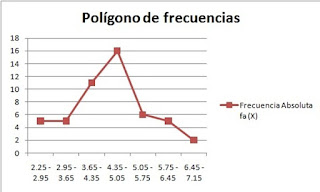
Polígonos de frecuencias
Para construir polígonos de frecuencias, se trazan las frecuencias absolutas o relativas de los valores de la variable en un sistema de ejes cartesianos y se unen los puntos resultantes mediante trazos rectos. Con ello se obtiene una forma de línea poligonal abierta.
Los polígonos de frecuencias se utilizan preferentemente en la presentación de caracteres cuantitativos, y tienen especial interés cuando se indican frecuencias acumulativas. Se usan en la expresión de fenómenos que varían con el tiempo, como la densidad de población, el precio o la temperatura.
Gráficos de sectores
En los diagramas de sectores, también llamados circulares o de tarta, se muestra el valor de la frecuencia de la variable señalada como un sector circular dentro de un círculo completo. Por ello, resultan útiles particularmente para mostrar comparaciones entre datos, sobre todo en forma de frecuencias relativas de las variables expresadas en forma de porcentaje.
Pictogramas y cartogramas
Para aligerar la presentación de datos estadísticos, con frecuencia se recurre a imágenes pictóricas representativas del valor de las variables. Dos formas comunes de expresión gráfica de los datos son:
Los pictogramas, que muestran diagramas figurativos con figuras o motivos que aluden a la distribución estadística analizada (por ejemplo, una imagen antropomórfica para indicar tamaños, alturas u otros).
Los cartogramas, basados en mapas geográficos que utilizan distintas tramas, colores o intensidades para remarcar las diferencias entre los datos.
Pictogramas
Cartograma
Pirámide de población
Otra forma corriente de presentación visual de datos estadísticos es la llamada pirámide de población.
Las pirámides de población se utilizan en la expresión de informaciones demográficas, económicas o sociales, y en ellas se clasifican comúnmente los datos de la población del grupo de muestra considerado en diferentes escalas de edad y diferenciada por sexo.
¿Qué es la probabilidad?
El término probabilidad proviene de lo probable, o sea, de aquello que es más posible que ocurra, y se entiende como el mayor o menor grado de posibilidad de que un evento aleatorio ocurra, expresado en una cifra entre 1 (posibilidad total) y 0 (imposibilidad absoluta), o bien en porcentajes entre el 100% o el 0%, respectivamente.
Para obtener la probabilidad de un suceso, generalmente se determina la frecuencia con la que ocurre (en experimentos aleatorios bajo condiciones estables), y se procede a realizar cálculos teóricos.
Para ello se sigue lo establecido por la Teoría de la probabilidad, una rama de las matemáticas dedicada al estudio de la probabilidad. Esta disciplina es largamente empleada por otras ciencias naturales y sociales como disciplina auxiliar, ya que les permite manejar escenarios posibles con base a generalizaciones.
El origen de la probabilidad reside en la necesidad del ser humano de anticiparse a los hechos, y de predecir en cierta medida el futuro. Así, en su empeño por percibir patrones y conexiones en la realidad, se enfrentó constantemente al azar, o sea, a lo que carece de orden.
Las primeras consideraciones formales sobre esta materia provienen del siglo XVII, específicamente de la correspondencia entre Pierre de Fermat y Blaise Pascal en 1654, o de los estudios de Christiaan Huygens en 1657 y de la Kybeia de Juan Caramuel en 1649, texto hoy en día perdido.
Tipos de probabilidad
Existen los siguientes tipos de probabilidad:
Frecuencial. Aquella que determina la cantidad de veces que un fenómeno puede ocurrir, considerando un número determinado de oportunidades, a través de la experimentación.
Matemática. Pertenece al ámbito de la aritmética, y aspira al cálculo en cifras de la probabilidad de que determinados eventos aleatorios tengan lugar, a partir de la lógica formal y no de su experimentación.
Binomial. Aquella en la que se estudia el éxito o fracaso de un evento, o cualquier otro tipo de escenario probable que tenga dos posibles resultados únicamente.
Objetiva. Se denomina así a toda probabilidad en la que conocemos de antemano la frecuencia de un evento, y simplemente se dan a conocer los casos probables de que ocurra dicho evento.
Subjetiva. Contrapuesta a la matemática, se sustenta en ciertas eventualidades que permiten inferir la probabilidad de un evento, aunque alejada de una probabilidad certera o calculable. De allí su subjetividad.
Hipergeométrica. Aquella que se obtiene gracias a técnicas de muestreo, creando grupos de eventos según su aparición.
Lógica. La que posee como rasgo característico que establece la posibilidad de ocurrencia de un hecho a partir de las leyes de la lógica inductiva.
Condicionada. Aquella que se emplea para comprender la causalidad entre dos hechos distintos, cuando puede determinarse la ocurrencia de uno tras la ocurrencia del otro.
Ejemplos de probabilidad
La probabilidad se halla continuamente a nuestro alrededor. Los ejemplos más obvios de ella tienen que ver con juegos de azar: los dados, por ejemplo. Es posible determinar la frecuencia de aparición de cada cara, a partir de una serie continua de lanzamientos del dado. O también puede hacerse con la lotería, aunque ello exige cálculos tan enormes que, virtualmente, los hace imposibles de predecir.
También lidiamos con la probabilidad cuando consultamos el pronóstico del tiempo, y se nos advierte un cierto porcentaje de probabilidad de lluvia. Dependiendo de la cifra, será más o menos probable que llueva, pero podría ocurrir que no suceda, dado que se trata de una predicción, no de una certeza.
Fórmula para calcular la probabilidad
El cálculo de las probabilidades se lleva a cabo según la fórmula siguiente:
Probabilidad = (Casos favorables / casos posibles ) * 100 (para llevarlo a porcentaje)
Así, por ejemplo, podemos calcular la probabilidad de que una moneda salga cara en un único lanzamiento, pensando que sólo puede salir una cara (1) de las dos que hay (2), esto es:
(1 / 2) * 100 = 50% de probabilidad.
En cambio, si decidimos calcular cuántas veces saldrá la misma cara en dos lanzamientos seguidos, deberemos pensar que el caso favorable (cara y cara o sello y sello) es uno entre cuatro posibilidades de resultado (cara y cara, cara y sello, sello y cara, sello y sello). Por ende:
(1 / 4 )* 100 = 25% de probabilidad.
Aplicaciones de la probabilidad
El cálculo de la probabilidad tiene numerosas aplicaciones en la vida cotidiana, como son:
El análisis de riesgo empresarial. Según el cual se estiman las posibilidades de caída de precio de las acciones bursátiles, y se intenta predecir la conveniencia o no de la inversión en una u otra empresa.
El análisis estadístico de la conducta. De importancia para la sociología, emplea la probabilidad para evaluar la posible conducta de la población, y así predecir tendencias de pensamiento o de opinión. Es común verlo en las campañas electorales.
La determinación de garantías y seguros. Procesos en los que se evalúa la probabilidad de avería de los productos o la fiabilidad de un servicio (o de un asegurado, por ejemplo), para así saber cuánto tiempo de garantía conviene ofrecer, o a quiénes conviene asegurar y por cuánto.
En la ubicación de partículas subatómicas. Según el Principio de Incertidumbre de Heisenberg, el cual establece que no podemos saber dónde está una partícula subatómica en un momento determinado y al mismo tiempo a qué velocidad se mueve, de modo que los cálculos en la materia se realizan normalmente en términos probabilísticos: existe X por ciento de probabilidades de que la partícula esté allí.
En la investigación biomédica. Se calculan porcentajes de éxito y de fracaso de las drogas médicas o de las vacunas, para así saber si son fiables o no, y si conviene o no producirlas en masa, o a qué porcentaje de la población podrán causarle determinados efectos secundarios.






No hay comentarios:
Publicar un comentario