Sea
una matriz A definida, a continuación, se puede obtener su determinante
dividiendo la matriz en tres matrices más pequeñas, en este caso matrices de
2x2. Para ello se elimina un renglón y una columna, de tal manera que los
elementos restantes formen una matriz de 2x2.
Iniciaremos con el primer renglón y la primera
columna:
El
determinante adoptará la siguiente fórmula, multiplicando el elemento por el
determinante de la matriz resultante:
Ahora con el siguiente
elemento:
Agregamos a la operación para obtener el
determinante:
Y se completa la fórmula del
determinante:
Ahora con un ejemplo:
Utilizando el procedimiento y fórmula
obtenemos el determinante:

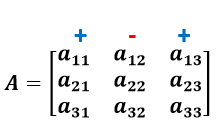





Gracias, me ayudó bastante.
ResponderEliminar